- Autor Matthew Elmers [email protected].
- Public 2024-01-11 06:34.
- Viimati modifitseeritud 2025-06-01 06:24.
Selles artiklis püüame mõista Bayerni, Rivenge'i ja Pennsylvania lahingulaevade relvade soomuste läbitungimist, samuti Saksa, Ameerika ja Briti soomukite võrdlevat kvaliteeti. Seda on äärmiselt raske teha, sest andmed Ameerika 356 mm, Saksa 380 mm ja Briti 381 mm kahurite kohta on väga visandlikud ja puudulikud ning mõnikord üksteisega vastuolus, kuid proovime siiski.
Milles täpsemalt probleem on? Vaatame, kuidas enamik mereväe (ja mitte ainult) ajaloo fänne võrdleb teatud relvade soomukite läbitungimist. Näiteks: ühes väljaandes, mis on pühendatud näiteks inglise dreadnoughtile, on teavet, et Esimese maailmasõja aegne Briti 381 mm mürsk läbistas umbes 70 kaabli kaugusel 381 mm soomusplaadi. Teises väljaandes, mis on pühendatud juba Saksa "pealinna" laevadele - et sarnane Saksa 380 mm mürsk "valdas" 350 mm soomust ainult 67, 5 kaabliga. Sellest näib järelduvat, et Inglise kahur on võimsam - just selline järeldus tehti.
Kuid tegelikult on selliste andmete võrdlemine sellisel viisil väga lihtne jama.
Kas ülaltoodud andmed on saadud tegeliku tulistamise tulemusena või on need arvutatud soomuste läbitungimismeetodite abil? Kui need on tegeliku laskmise tulemused, kas tingimused olid mõlema relva puhul identsed? Kui soomuste läbitungimine saadi arvutuste abil, siis kas kasutati samu meetodeid? Kas saadud andmed on vastavate ministeeriumide ja osakondade spetsialistide töö tulemus või on see kalkulaatori kasutusele võtnud ajaloolaste arvutuste tulemus? On selge, et teisel juhul on täpsus palju väiksem … Näidete jaoks ei pea te kaugele minema: võtame S. Vinogradovi kuulsa monograafia "Teise Reichi" Superdreadnoughts of Bayern "ja" Baden " ". Lisas nr 2 austas lugupeetud ajaloolane koos V. L. Kofman teeb palju arvutusi, et võrrelda lahingulaevade Rivenge ja Bayern võimalusi. Kuid kahjuks piisab, kui vaadata 15-tolliste relvade parameetrite tabelit (lk 124) ja me näeme, et lugupeetud autorite arvutuste kohaselt on inglise 381 mm püstol, mille tõusunurk on 20, 25 kraadi ulatuses on ainult 105 kaablit, see tähendab umbes 19, 5 tuhat m. Kui välismaised allikad sama algkiiruse (732 m / s) ja veidi madalama tõusunurga (20 kraadi) jaoks annavad oluliselt suuremad vahemaad - 21, 3-21, 7 tuhat m. Loomulikult mõjutavad sellised kõrvalekalded tegelikest väärtustest kõige negatiivsemalt arvutuste tulemusi.
Kuid isegi kui allikad esitavad spetsialistide arvutuste tulemusi, mille täpsuses pole kahtlust, tekib veel üks võrdlust raskendav tegur: siin on küsimus soomukite kvaliteedis. On selge, et needsamad britid kasutasid soomuste läbitungimise arvutamisel konkreetse dreadnought'i kavandamisel Briti soomukite vastavaid näitajaid, sakslased - vastavalt saksa jne. Ja eri riikide soomused võivad vastupidavuse poolest erineda, kuid see on siiski pool hädast: lõppude lõpuks täiustati ühes riigis sama Kruppi soomust pidevalt. Seega selgub, et näiteks Inglismaal tehtud ja ilmselt sama Kruppi raudrüü jaoks tehtud, kuid eri aegadel tehtud suurtükisüsteemide arvutused võivad osutuda võrreldamatuks. Ja kui siia lisada veel peaaegu täielik tõsise töö puudumine soomukijuhtumi arengus erinevates maailma riikides …
Üldiselt pole soomuste läbitungimise enam -vähem usaldusväärne võrdlus nii lihtne ülesanne, kui esmapilgul võib tunduda. Ja sõbralikul moel on võhikul (kes kahtlemata on selle artikli autor) parem seda asja mitte ette võtta. Aga kahjuks - meie sügavaks kahetsuseks ei kiirusta profid nende probleemidega kuidagi tegelema, nii et … nagu öeldakse, tembeldatud paberi puudumisel kirjutame lihttekstina.
Loomulikult ei ole enam võimalik ülalnimetatud suurtükisüsteemide täiemahulisi katseid läbi viia, seega on meie saatus arvutused. Ja kui jah, siis on vaja öelda vähemalt paar sõna soomuste läbitungimisvalemite kohta. Kui avaldatakse kaasaegsed arvutusmeetodid, siis ainult suletud väljaannetes ja populaarses kirjanduses on tavaliselt toodud Jacob de Marri valem. Huvitav on see, et mereväeakadeemia professor L. G. Gontšarov nimetas seda oma 1932. aasta suurtükiväeõpikus Jacob de Marri valemiks. See valem koos paljude teistega oli eelmise sajandi alguses laialt levinud ja pean ütlema, et see on üsna täpne - võib -olla on see isegi kõige täpsem nende aastate sarnaste valemite hulgas.
Selle eripära seisneb selles, et see ei ole füüsiline, see tähendab, et see ei ole füüsikaliste protsesside matemaatiline kirjeldus. De Marri valem on empiiriline, see peegeldab rauast ja teras-raud-raudrüü eksperimentaalse koorimise tulemusi. Vaatamata sellele "ebateaduslikule olemusele" näitas de Marri valem paremaid laskmisi ja Kruppi raudrüüde tulemusi kui teised levinud valemid ja seetõttu kasutame seda arvutuste tegemiseks.
Huvilised leiavad selle valemi käesoleva artikli lisast, kuid pole vaja sundida kõiki, kes seda materjali loevad, seda mõistma - see ei ole vajalik artikli järelduste mõistmiseks. Märgime ainult, et arvutuses kasutatakse väga lihtsaid ja kõigile sõjaväelaevastike ajaloost huvitatud tuttavaid mõisteid. Need on mürsu mass ja kaliiber, soomuse paksus, mürsu soomusesse tabamise nurk, samuti mürsu kiirus soomusplaati tabades. Kuid de Marr ei saanud muidugi piirduda ülaltoodud parameetritega. Lõppude lõpuks sõltub mürsu läbitungimine mitte ainult selle kaliibrist ja massist, vaid ka teatud määral selle kujust ja terase kvaliteedist, millest see on valmistatud. Ja soomusplaadi paksus, millest mürsk suudab üle saada, sõltub muidugi mitte ainult mürsu jõudlusest, vaid ka soomuki kvaliteedist. Seetõttu võttis de Marr valemisse sisse spetsiaalse koefitsiendi, mis on tegelikult mõeldud soomuse ja mürsu näidatud omaduste arvestamiseks. See koefitsient tõuseb koos soomuse kvaliteedi tõusuga ja väheneb mürsu kuju ja kvaliteedi halvenemisega.
Tegelikult seisneb erinevate riikide suurtükisüsteemide võrdlemise peamine raskus just sellel koefitsiendil, mida me tulevikus lihtsalt nimetame (K). Peame selle leidma iga ülaltoodud tööriista puhul - kui muidugi tahame mõnevõrra õiget tulemust saada.
Niisiis, võtame kõigepealt üsna laialdased andmed Saksa 380 mm / 45 relva "Bayern" soomuste läbitungimise kohta, mille kohaselt võis relv 12 500 m kaugusel (need samad 67, 5 kaablit) läbida 350 mm raudrüü. 750 kg kaaluva mürsu parameetrite leidmiseks kasutame ballistilist kalkulaatorit, mille algkiirus on soomusele löögi hetkel 800 m / s: selgub, et selline mürsk tabab rangelt vertikaalselt paigutatud soomusplaati nurk 10, 39 kraadi, kiirusega 505, 8 m / sek. Väike lahtiütlemine - edaspidi, kui räägime mürsu lööginurgast, peame silmas nn "nurka normaalsest". "Normaalne" on siis, kui mürsk tabab bonnepliiti selle pinnaga rangelt risti, see tähendab 90 -kraadise nurga all. Vastavalt sellele tabas mürsk 10 -kraadise nurga all.tavalisest tähendab, et see tabas plaati 80 -kraadise nurga all. selle pinnale, kaldudes "võrdlusest" 90 kraadi. 10 kraadi võrra.
Aga tagasi Saksa relva soomukite läbitungimise juurde. Koefitsient (K) on sel juhul ligikaudu (ümardatud lähima täisarvuni) võrdne 2083 -ga - seda väärtust tuleks pidada Esimese maailmasõja ajastu soomuste puhul täiesti normaalseks. Kuid siin tekib üks probleem: fakt on see, et raudrüüde läbitungimise andmete allikaks on raamat "Teise maailmasõja Saksa pealinnalaevad", kus Bayerni 380 mm / 45 relva võrreldi lahingulaeva peamise kaliibriga "Bismarck". Ja kas ei võiks olla nii, et arvutamisel võeti arvesse kahe maailmasõja vahelisel ajal loodud soomuki Krupp näitajaid, mis oli palju tugevam kui see, mis paigaldati Bayenne'i, Rivenge'i ja Pennsylvaniale? Veelgi enam, elektrooniline entsüklopeedia navweaps teatab, et on tõendeid selle kohta, et 20 000 m kaugusel suutsid Saksa 380 mm kestad läbida 336 mm soomusplaadi ja me räägime Esimese maailmasõja ajastu soomustest.
Noh, me usume: 20 km juures on langemisnurk 23,9 kraadi, mürsu kiirus soomukil 410,9 m / s ja koefitsient (K) - mõni kahetsusväärne 1618, mis ei sobi soomusse vastupanuväärtused kogu Esimese maailmasõja ajastul. Sarnane tulemus lähendab üldiselt Saksamaal toodetud Kruppi soomust homogeensele soomustakistusele … Ilmselgelt sisaldavad navweapsi andmed mingisugust viga.
Proovime siis kasutada mõnda muud teabeallikat. Siiani oleme kasutanud arvutatud andmeid ja nüüd proovime neid võrrelda Saksa 380 mm / 45 kahuri tegelike katsete tulemustega: need on andnud S. Vinogradov ülalmainitud saksa keelele pühendatud monograafias. lahingulaevad.
See kirjeldab soomust läbistavate mürskudega tehtud kolme lasu tagajärgi 200, 290 ja 450 mm paksuste soomusplaatide vastu, millest viimane on meie jaoks kõige huvitavam: 734 kg kaaluv mürsk tabas soomusplaati 0 nurga all. (st 90 kraadi pinna suhtes) ja kiirusega 551 m / s löödi 450 mm läbi plaadi. Sarnane tulemus vastab koefitsiendile (K) 1 913, kuid tegelikult on see pisut madalam, sest sakslased leidsid oma mürsu koguni 2530 m kaugusel selle läbistatud takistuse taga ja - üldiselt. Kahjuks, kui puuduvad andmed selle kohta, kui palju sellest kaugusest lendas mürsk läbi õhu, kui palju - "sõitis" maapinnal, on absoluutselt võimatu määrata selle salvestatud energiat pärast soomuste läbitungimist.
Võtame nüüd Briti 381 mm / 42 suurtükisüsteemi. Kahjuks on andmed selle soomukite läbitungimise kohta üsna ebamäärased: näiteks V. L. Kofman, mainitakse tõsiasja, et need Briti relvad läbistasid soomukid, oma kaliibri paksused umbes 70 kaabli kaugusel. Aga millise mürsuga ja millise algkiirusega? Võttes arvesse asjaolu, et viide sisaldub lahinguristleja "Hood" pühendatud monograafias ja viitab selle laeva loomise perioodile, võib eeldada, et me räägime 871 kg kestast. Siin tekib aga veel üks küsimus: sellise mürsu ametlik algkiirus oli 752 m / s, kuid mõned brittide arvutused viidi läbi väiksema kiirusega 732 m / s, siis millist väärtust peaksime võtma? Kuid olenemata sellest, millist näidatud kiirust me kasutame, kõigub koefitsient (K) vahemikus 1 983-2 048 ja see on suurem kui saksa relva väärtuse (K) puhul. Võib arvata, et see räägib Briti soomukite kvaliteedi paremusest võrreldes Saksa omadega … või on see, et Saksa mürsu geomeetriline kuju sobis paremini soomuste läbistamiseks? Või äkki on kogu asi selles, et V. L. Kofmanid on arvutatud väärtused, kuid kas praktikas saavutaksid Briti kestad parema tulemuse?
Noh, meie käsutuses on andmed lahingulaeva "Baden" tulistamise tulemuste kohta

Niisiis, üks Briti kestadest, lööb 18 -kraadise nurga all. kiirusega 472 m / sek., "ületas" Saksa põhikaliibriga torni 350 mm esisoomuse. Need andmed on seda väärtuslikumad, et sellisel juhul ei ole kestnud mitte Briti, vaid Saksa soomukid, st 381 mm / 42 ja 380 mm / 45 relvade katsed on seega ühes koordinaatsüsteemis.
Paraku ei aita nad meid liiga palju. Kui eeldada, et inglise kest läbistas Saksa torni, nagu öeldakse, „viimase jõuga” ja kui soomuseid oleks 351 mm, oleks see ebaõnnestunud, oleks tema (K) võrdne 2021 -ga. Muide, huvitav on see, et S. Vinogradov väidab, et Briti mürsku, mis tungis Saksa torni 350 mm esisoomustesse, hiljem ei leitud, kuid tegelikult on raportis märgitud midagi muud - see plahvatas ja seal on kirjeldus, kuhu killud tornis lendasid.
Loomulikult ei ole meil absoluutset alust eeldada, et see läbitung oli 381 mm mürsu piir või isegi selle lähedal. Kuid sellegipoolest võib mõne kaudse märgi järgi eeldada, et see oli täpselt nii. Sellele vihjab veel üks tabamus: Suurbritannia 871 kg mürsk tabas 350 mm barbetti 11 kraadise nurga all, ehkki suutis soomukisse teha augu läbimõõduga 40 cm, ei sattunud see barbeti sisse ise, lõhkedes soomukite ületamise protsessis. Sel juhul tabas tabamust peaaegu barbeti keskosa, see tähendab soomusplaadi kõverus, kui see mingil määral mõjutas, oli see minimaalne.
Kõigest eelnevast võib proovida teha mõningaid järeldusi, kuid tõendusbaasi nõrkuse tõttu on need loomulikult väga oletuslikud.
Järeldus 1: Esimese maailmasõja aegsed Saksa soomukid vastasid vastupidavuse poolest brittidele. See järeldus kehtib, kui V. L. Kofman, et Suurbritannia 381 mm / 42 relv oli võimeline läbima selle kaliibriga võrdseid soomuseid 70 kbt võrra ja kui me ei eksi eelduses, et Saksa torni esiplaadi 350 mm läbitungimine 18 nurga all kraadi ja kiirus 472 m / s … on Briti 381 mm mürsu läbitungimispiir või väga lähedal sellele.
Järeldus 2. Ilmselt pakkus Saksa 380 mm mürsu kuju ja kvaliteet selle soomuste parema läbitungimise kui inglise oma. Ülaltoodud andmete põhjal võime eeldada, et Briti 381 mm mürsu koefitsient (K) Saksa soomukit tulistades oli umbes 2000, Saksa 380 mm mürsk aga umbes 1900. Kui meie esimene on õige, võib järeldada, et Briti ja Saksa soomukite soomustakistus on ligikaudu samaväärne, on ilmne, et madalama koefitsiendi (K) ainus põhjus võib olla ainult mürsk ise.
Miks võiks Saksa kest parem olla? Selle kaliiber on pisut väiksem, ühe millimeetri võrra, kuid loomulikult ei saa see vaevalt märkimisväärset mõju avaldada. Arvutus näitab, et sama massi (750 kg) korral toob kaliibri muutmine 1 millimeetri võrra kaasa soomuste läbitungimise suurenemise 1,03 millimeetri võrra. Saksa mürsk on ka lühem - selle pikkus oli 3,5 kaliibrit, samas kui Briti "Greenboy" pikkus on 4 kaliibrit. Võib -olla oli ka muid erinevusi. Muidugi mängib siin olulist rolli terase kvaliteet, millest mürsk valmistatakse.
Arvutame nüüd Saksa ja Briti relvade soomuste läbitungimise 75 kaabli kaugusele - üldtunnustatud vahemaa otsustavaks lahinguks, kus võis oodata piisavalt tabamusi liini vaenlase laeva hävitamiseks.
Näidatud vahemaa tagant tabas 871 kg Briti 381 mm / 42 suurtüki mürsku, mis tulistati algkiirusel 752 m / s, vertikaalselt asetatud soomusplaati 13,05 kraadise nurga all ja selle kiirus "plaadil" oli 479,6 m / s … Kui (K) on võrdne 2000 -ga, oli Jacob de Marri valemi järgi Briti mürsu soomuste läbitungimine 376, 2 mm.
Mis puutub Saksa kesta, siis kõik on natuke keerulisem. Kui meie järeldus, et see ületas soomukite läbitungimise osas inglise keele, on õige, siis olid Saksa 380 mm / 45 relva võimalused 75 kaablil väga lähedased inglise viieteist tollisele püstolile. Sel kaugusel tabas Saksa 750 kg mürsk sihtmärki 12,42 kraadise nurga all kiirusel 482,2 m / s ja (K), mis võrdus 1900 -ga, oli soomuste läbitungivus 368,9 mm. Aga kui selle artikli autor eksib endiselt ja Saksa relva puhul tasub kasutada sama koefitsienti nagu inglise relva puhul, siis 380 mm mürsu võimalused langevad 342,9 mm-ni.
Sellegipoolest on autori sõnul Saksa mürsu soomuste läbitungimine kõige lähemal 368, 9 mm -le (lõppude lõpuks andis praktiline tulistamine koefitsiendi 1913, hoolimata asjaolust, et mürsk lendas siis 2,5 km), kuid soomukite läbitungimine Inglise mürsu arvutus võib olla pisut madalam. Üldiselt võib arvata, et 75 kaabli kaugusel on Briti ja Saksa suurtükisüsteemid soomuste läbitungimise osas üsna võrreldavad.
Kuid Ameerika 356 mm / 45 relvaga osutus kõik palju huvitavamaks. Varem viidatud andmeid 680 kg kaaluvate kestade kohta tuleks venekeelses kirjanduses pidada kanooniliseks.
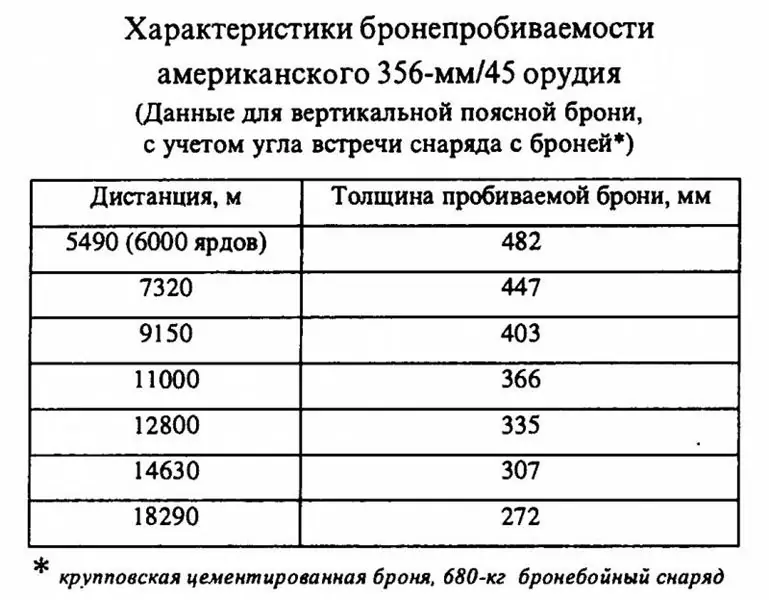
Tegelikult näivad selles märgitud väärtused viivat täiesti ilmsete järeldusteni: isegi kui USA-s pärast 1923. aastat ilmunud 680 kg kestad on soomuste läbitungimisest madalamad kui nende 380-381 mm eurooplased.” kolleegid ", siis mida tegelikult rääkida varasematest 635 kg kestadest, mis olid varustatud 356 mm Ameerika suurtükiväe suurtükiväega! Need on kergemad, mis tähendab, et nad kaotavad lennukiiruse kiiremini, samas kui nende algkiirus ei ületanud raskemaid kestasid ning kuju ja kvaliteedi osas peaks 1923. aasta laskemoon olema eelis. On selge, nagu päev, et Ameerika "Pennsylvania" oli kasutuselevõtmise ajal soomukite sissetungimise osas madalam kui Briti ja Saksa karded. Noh, see on ilmselge, kas pole?
Just sellise järelduse tegi autor, arvestades Ameerika neljateist tolliste relvade võimeid artiklis "Standard" USA, Saksamaa ja Inglismaa lahingulaevad. Ameerika "Pennsylvania" ". Ja siis võttis ta kalkulaatori …
Fakt on see, et de Marra valemi järgi tehtud arvutused näitasid, et Ameerika 356 mm / 45 relvade soomuste läbitungimise tabelis oli koefitsient (K) võrdne 2317! Teisisõnu, tabelis näidatud Ameerika 680 kg mürsud näitasid tulemusi, kui nad olid kokku puutunud soomustega, mis ei loodud Esimese maailmasõja ajastul, vaid palju hilisemate ja vastupidavamate proovidega.
Kui palju on soomuskaitse tugevus esimese ja teise maailmasõja vahelisel ajal suurenenud, on raske öelda. Venekeelsetes allikates leidub sellele küsimusele vaid põgusaid ja sageli vastuolulisi viiteid, mille põhjal võib eeldada, et Kruppi soomuse tugevus on suurenenud umbes 20-25%. Seega on esimese maailma ajastu suure kaliibriga kestade puhul koefitsiendi (K) kasv 1900-2000 kuni 2280-2500, kuid siin tuleb meeles pidada, et soomuskaitse kvaliteedi paranemisega muidugi tõusis ka mürskude kvaliteet ja seetõttu võib Teise maailmasõja raske laskemoona puhul (K) olla vähem. Seetõttu tundub (K) summas 2317 sõjajärgsete kestade puhul, mis on loomulikult varem omandatud kogemusi arvesse võttes täiustatud, üsna orgaaniline, kuid Teise maailmasõja ajastu soomukite jaoks mitte esimene.
Kuid seades koefitsiendi (K) ameerika 680 kg kestade tasemele 2000, st viies soomuskaitse kvaliteedi Esimese maailmasõja ajastusse, saame 75 kaabli kaugusele soomuse läbitungimine tasemel 393,5 mm, see tähendab kõrgem kui Briti ja Saksa viieteistkümne tollistel püssidel!

Üleminek 635 kg mürsule annab väga ebaolulise paranduse - ballistiline kalkulaator näitas, et 75 kaabli kaugusel, langemisnurgaga 10, 82 kraadi. ja kiirus "soomukil" 533, 2 m (K) juures võrdub 2000, Ameerika mürsk tungib läbi Esimese maailmasõja ajastu soomuki, paksusega 380 mm, see tähendab oluliselt rohkem kui tema enda kaliiber!
Teisest küljest on täiesti võimalik, et selline arvutus pole ikka veel täiesti õige. Fakt on see, et mõnede aruannete kohaselt väheneb sama soomuse koefitsient (K) mürsu kaliibri suurenemisega. Näiteks meie arvutustes on Saksa 380 mm / 45 suurtükiväesüsteemi maksimaalne väärtus (K), mis on saadud arvutuste abil ja avaldatud allikates, 2083. Samal ajal arvutatakse Saksa 305 mm / 50 relva, mis paigaldati Kaiserlichmarine'i laevadele, alustades Heligolandidest, annavad soomuste läbitungimise allikate andmed (K) tasemele 2145. Seega on võimalik, et 356 mm / 45 relva (K) = 2000 Võtsime arvesse Ameerika relvade soomuste läbitungimise arvutamist, on endiselt liiga väike.
Lisaks pole autoril kahjuks mingeid "vihjeid", millega võrrelda ameeriklaste Kruppi soomukite soomustakistust Euroopa kolleegidega. Ei jää muud üle, kui pidada seda samaväärseks saksa ja inglise soomuskaitsega, kuigi see muidugi ei pruugi nii olla.
Võtame kokku kõik need üsna kaootilised andmed. Võttes arvesse arvutustes kasutatud "meetodite" vigu, võib suure tõenäosusega eeldada, et Lahingulaevade Rivenge, Bayern ja Pennsylvania peamiste kaliibripüstolite vertikaalse soomuskaitse soomuste läbitungimine 75 kaabli kaugusel oli ligikaudu sama ja ligikaudu 365-380 mm.
Hoolimata hulgast eeldustest võimaldavad meie käsutuses olevad andmed siiski teha mõningaid järeldusi vertikaalse soomuskaitse kohta. Kuid horisontaalsete tõkete, mis on soomustekid, murdmisega on kõik palju keerulisem. Fakt on see, et Jacob de Marr ei vaevunud kahjuks üldse looma valemit horisontaalse kaitse tugevuse määramiseks. Selle põhivalem, mis on kohandatud kaasaegsetele soomustüüpidele, sobib ainult üle 75 mm paksuse tsementeeritud soomuse arvutamiseks. See valem on toodud käesoleva artikli lisas nr 1 ja kõik selle artikli varasemad arvutused tehti seda kasutades.
Kuid nende aastate laevade tekke kaitses mitte tsementeeritud (heterogeenne), vaid homogeenne raudrüü, millel puudus pinnakarastatud kiht. Sellise soomuse (kuid - vertikaalselt paigaldatud!) Puhul kasutatakse teistsugust valemit, mis on ette nähtud tsementeerimata soomusplaatide hindamiseks paksusega alla 75 mm, see on toodud lisas nr 2.
Tahaksin märkida, et mõlemad need valemid on võetud enam kui tõsisest allikast: „Mereväe taktika käik. Suurtükivägi ja raudrüü 1932, autor - RKKA mereväeakadeemia professor L. G. Gontšarov, üks sõjaeelse NSV Liidu juhtivaid eksperte mereväe suurtükiväe alal.
Ja kahjuks ükski neist ei sobi horisontaalse kaitse vastupidavuse hindamiseks. Kui kasutame tsementeeritud soomuste valemit, siis 75 kaabli kaugusel saame vähese soomuse läbitungimise: 46,6 mm 381 mm / 42 Briti jaoks, 39,5 mm 380 mm / 45 saksa jaoks ja 33,8 mm 356 mm / 45 ameeriklase jaoks relvad. Kui kasutame tsemendita soomuste jaoks teist valemit, siis saame, et kui tabada 75 kaabli kaugusele tüüpilise nurga all, tungivad kõik kolm suurtükisüsteemi hõlpsalt läbi 74 mm soomusplaadi, mis säilitab tohutu kineetilise energiavaru - Näiteks inglise 381 mm, mürsk, mis tungib 75 mm kaabli kaugusel sellise paksusega soomustesse, on kiirusega 264,5 m / s, samas kui selle kiirus on 482,2 m / s. Kui me ignoreerime soomusplaadi paksuse piirangut, selgub, et Briti 381-mm mürsk on vastavalt ülaltoodud valemile võimeline tungima üle 180 mm paksuse teki soomuse! Mis on muidugi täiesti võimatu.
Kui me püüame viidata Bayerni klassi lahingulaeva katsetulemustele, näeme, et soomust läbistavad 871 kg briti kestad tabasid kaks korda tornide horisontaalset soomust, mille paksus oli 11 kraadi nurga all 100 mm., mis vastab kaugusele 67,5 kaablit mürsule algkiirusega 752 m / s ja 65 kaablit - mürsule algkiirusega 732 m / s. Mõlemal korral soomust läbi ei torgatud. Kuid ühel juhul tegi mürsk rikošetiga soomustesse soone, mille sügavus oli 70 cm, see tähendab, et plaat oli väga tugevalt painutatud. Ja teises, kuigi kest oli jällegi rikošett, ei olnud soomus mitte ainult 10 cm nõgus, vaid ka rebenenud.

Kahju sarnane iseloom viitab sellele, et kuigi Saksa 100 mm soomuk pakkus kaitset näidatud vahemaadel, oli see kui mitte võimaliku piiri piires, siis sellele väga lähedal. Kuid tsementeeritud soomuste valemi järgi tehtud arvutused annavad soomuste läbitungimise ainult 46,6 mm suuremal kaugusel, kus langemisnurk on suurem, ja seega oleks mürsul kergem tungida teki soomustesse. See tähendab, et valemi kohaselt selgub, et 100 mm tekil oleks pidanud naljalt ja suure turvavaruga peegelduma inglise kestad - praktika seda siiski ei kinnita. Samal ajal selgub arvutustest, mis kasutavad tsementeerimata soomuste valemit, et Badeni põhikaliibri katused oleks pidanud kergesti läbistama ja - suure kooreenergiaga -, mis jällegi ei ole praktikaga üldse kinnitatud.
Pean ütlema, et sellistel arvutuste ebatäpsustel on täiesti loogiline seletus. Nagu me varem ütlesime, ei ole de Marri valemid füüsikaliste protsesside matemaatiline kirjeldus, vaid on vaid raudrüü testimisel saadud mustrite fikseerimine. Kuid testiti vertikaalset soomuskaitset, mitte horisontaalset, ja pole sugugi üllatav, et antud juhul mustrid lihtsalt lakkavad töötamast: horisontaalselt paiknevate soomuste puhul, mille kestad põrkasid oma pinna suhtes väga väikese nurga all, need mustrid, on muidugi täiesti erinevad.
Selle artikli autor kohtas "Internetis" arvamusi, et de Marri valemid toimivad tõhusalt normaalsest kõrvalekaldumise nurkades mitte rohkem kui 60 kraadi, see tähendab 30 kraadi plaadi pinnast ja muust. Võib arvata, et see hinnang on tõele väga lähedal.
Seega peame kahetsusega tõdema, et autori käsutuses olev matemaatiline aparaat ei võimalda teha usaldusväärseid arvutusi lahingulaevade Rivenge, Bayern ja Pennsylvania horisontaalse kaitsetakistuse kohta. Eespool öeldut silmas pidades on raske kasutada erinevates allikates esitatud andmeid horisontaalse soomuki soomuste läbitungimise kohta - reeglina põhinevad need kõik samadel arvutustel de Marri valemite järgi ja on valed.






